零基础微积分入门基本教程

本文已被读次

2023 年 1 月 27 日更新：

本文正在施工中，将原作业部落的文章迁移到这里。
因为早年撰文不注意，本文中格式存在各种问题（如中英文标点乱用、数学符号不规范、中英文间无空格等等），需要修复完毕后才能继续更新，预计会于最近几天完成。敬请关注。

2023 年 2 月 13 日更新：

首次更新完成，修复了大部分格式问题，但仍有少量问题未修复，如有发现请在评论区指出，谢谢。
目前网站可能比较卡顿，考虑一下科学上网吧。

\[\lim_{学习 \to 坚持} 学习=成功\]

前言

非常高兴你能浏览到这篇文章。我也不太清楚我写作的动机，可能纯属兴趣使然吧。

参考书籍

《高等数学（第六版）》上册
同济大学数学系编
高等教育出版社出版
《7天搞定微积分》
石山平大上丈彦著李巧丽译
南海出版公司出版
《Principles of Mathematical Analysis》
Walter Rudin 著
McGraw-Hill Education 出版

我是否适合看下去?

在看这篇文章前，你至少需要掌握以下知识：

至少初中水平的数学应用能力
至少小学水平的阅读能力
耐心和对数学的热情
以上三条是扯淡
这条也是

What’s calculus?

在正式开始学习微积分前，首先我们得明白微积分是啥。

百度一下，我们很容易找到这样的描述：

微积分（Calculus）是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支。它是数学的一个基础学科。内容主要包括极限、微分学、积分学及其应用。微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

诶诶诶，别跑啊，我知道这种专家写出来的东西不是一般人能领会得了的。。

简单的说，微积分学是高等数学(并不是高中数学)的重要组成部分，它的地位，相当于小学的四则运算或是初中的方程运算。它非常奇怪、麻烦，可是在高等数学中，你时时刻刻都要用到它。

当然，人们不会故意发明奇怪、麻烦的东西来为难自己，它的应用十分广泛，我们在后面会慢慢提到。

它主要分成两个部分：微分和积分，它们相辅相成，虽各有变化却互为表里，是一对基佬兄弟。我们会在接下来的文章中分别讨论这两个东西。

废话不多说，马上上干货~~

一、导数

导数是微分学的主要内容。翻回去看看百度百科对导数的解释：

导数描述一个函数的变化率。

这是啥么意思呢？变化率是个什么东西？

1.1 First Blood —— 斜率

先来看个函数图像：

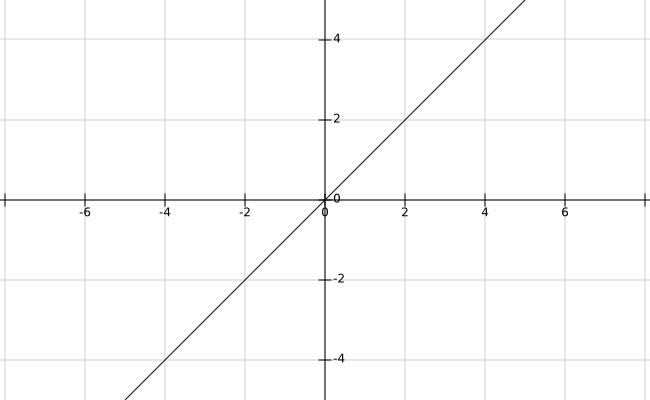
相信你一口就能报出这个函数的解析式：$$y=x$$

然后，我们再看个稍微复杂点的图像：

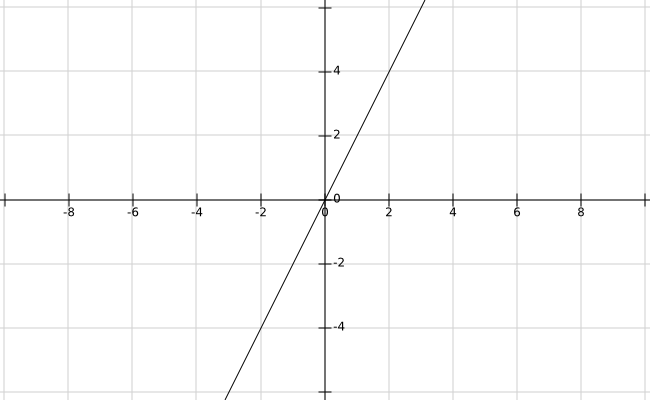
额，这哪里复杂了嘛！明明还是个一次函数啊。。。

不不不，差别大了去了，试试找出这两个函数图像的不同之处？

上下滚动页面，你应当能够看出图像倾斜程度存在着区别，有的数学老师也叫它「$k$ 决定函数陡平」啥啥的。

回忆一次函数的表达式:$$y = kx+b (k≠0)$$ 哈，所以上面这个式子里，**$k$值的大小就代表着图像倾斜程度的大小**，不是吗？

好了，你的头脑中已经有了基本的微分概念了，同学们，下课！

你的表情？哈哈，开个玩笑，还是先别急着关掉页面(从哪里能找到这么没节操的文章真是)。
不过这句话并没有问题，应当说，从初中学习函数开始，我们就有了对于这些知识的模糊概念，只是它们尚未发掘出来。~~所以这篇所谓的教程，其实就是帮助万恶的数学老师解决这些概念问题…~~

还是回到上面这个简单的例子。我们说$y=x$与$y=2x$这两个函数的倾斜程度不同，因为$y=2x$显得更”陡”一些。

虽然小明同学觉得这样描述很好，但是呢，数学家们就是不满足于「a 比 b 陡」这样听起来不是很清楚(~~也可能是因为他们语文阅读能力不行~~)的描述方式，(这样听起来不够炫酷狂霸拽)于是发明了一个很好(奇)听(怪)的名字用来描述一条线的陡峭程度，这就是————斜率。

当当！我们终于接触到了第一个数学定义。

呃…虽说这个定义还不完整，甚至你还没弄清啥意思，不过万事总有个开头的，是吧？

接下来我们将慢慢解释斜率这个听起来很高大上的名词。

既然说斜率是个数值，是数值就应该能被写出来。那么我们怎么表示它呢？

再再一次回到上面的例子。容易发现，当$k=2$时，图像明显比$k=1$时的要陡峭不少。继续画下去：$k=3、4、5、6、7...$ 图像会越来越陡。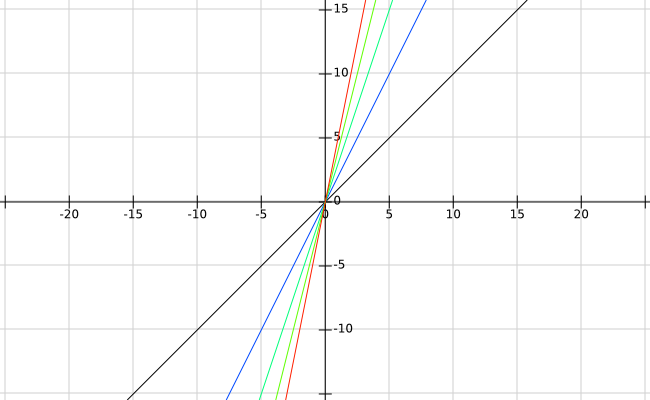不同颜色的直线对应了不同的 $k$ 我们发现，$k$值增大使得函数更陡峭。因此，对于一次函数，我们可以用k值大小来表示它的斜率。

这个定义听起来很唐突、很随意啊…高大上的感觉顿时都没有了…

更一般地说，斜率也可以这么得出:

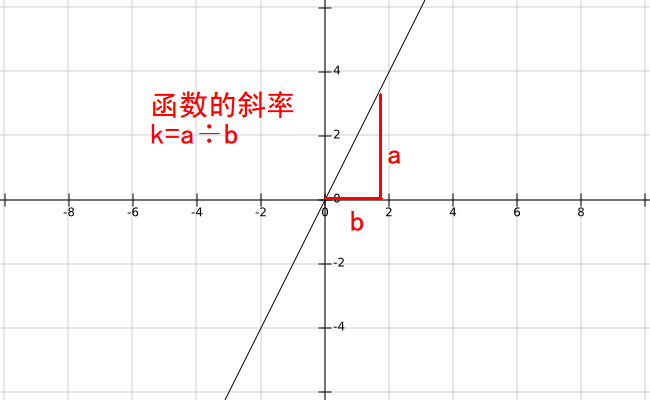
这样，我们对于斜率就有精确的定义了，它不再是一个模糊的概念，而是一个可以拿来比较大小的数值了。比方说，$y=2x$的斜率就是$2$。

你可能被这些概念搞得有点懵。重新强调一遍，斜率描述一条线的陡峭程度。而一次函数的$k$值越大，图像越陡，所以对于一次函数，我们可以用$k$值大小来描述它的斜率。

如果你就是没办法把$k$和斜率联系起来，稍微喘口气，再往下看吧。

1.1.1 [选读]斜率的严格定义

（对于初三及以上水平的读者，可以有选择性地阅读这些标有「[选读]」文字的部分，因为这些部分可以加深对一些知识的理解。如果你不想看，跳过也没关系。

警告：数学重灾区，请在监护人的陪同下观看。）

先看看百度百科上的斜率词条：

slope，又称「角系数」，是一条直线对于横坐标轴正向夹角的正切，反映直线对水平面的倾斜度。

图挂了，稍后修复如图，$直线P_1P_2$的斜率即为$k=\tan\alpha=\frac{y\_2-y\_1}{x\_2-x\_1}$。其中$α$又被称为倾斜角，取值范围为$0^\circ \leq \alpha<180^\circ$。

故：当直线的斜率存在时，斜截式$y=kx+b$，其斜率即为$k$。

1.2 点的斜率？

到现在为止，我们所讨论的函数都仅限于一次函数。你可能觉得数学家们真是一群闲得蛋疼的人，一个简单的$k$值都要起个难听的名字。况且，这和微积分有个卵关系？

别猴急，我们先来进一步讨论斜率的含义。在我们搞清楚这些基本概念前，空谈微积分是没啥意义的。

言归正传。对于二次函数或者反比例函数，又该如何表示它的斜率呢？

先来看看这个熟悉的二次函数吧。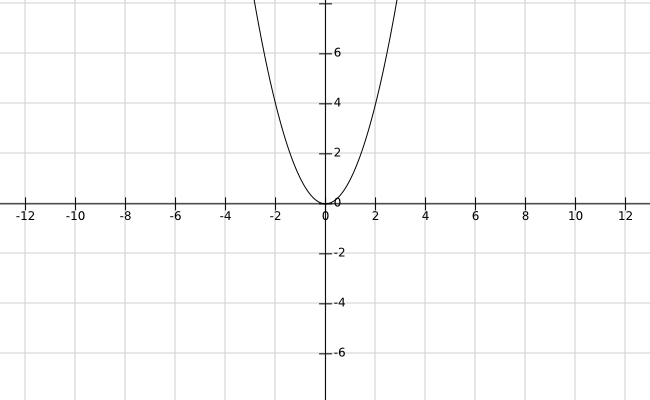相信这样简单的U型的函数，你已经非常熟悉了。但是，在表示它的斜率时，你会发现有点小麻烦，不，是大麻烦。

对于这个函数，我们还能用$k$值来表示它的倾斜程度吗？

稍做思考，你会发现行不通。这个函数的陡峭程度不是用一个”陡”或者”平”能描述得了的。它的图像自左向右，先是快速下降，再逐渐减缓，在原点处猛地拐了一个180度的大弯，又开始逐渐变快、飞速上升。

那么，显然它的整个图像的斜率已经无法直接表示了。我们是不是能求出其中一段的斜率呢？

比方说，在y轴右边的这半个曲线，如果只看从0到2这一小段，你会觉得它很像$y=2x$的一小段。

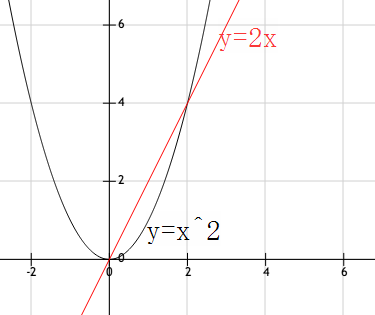
嘿，这一段的斜率是不是差不多是$2$呢？

不对。

唔，也不能说是全错，毕竟只是弯了点啊。。

所以让我们继续放大图像，取更小的区间试试？于是我们放大大大大大大大大大大大大大（此处省略 N 个大）

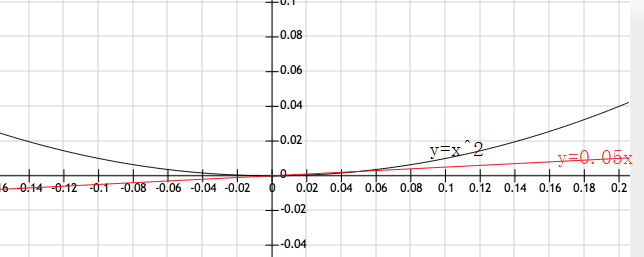
诶，这两个图像看起来有一部分重合了呢？！也不全然，毕竟前者是曲线，后者是直线呐。。显然，即使我们放大下去，两个图像也很难有相同的部分，或者说不可能有。看来硬凑直线的方法行不通，得换个思路。

咳，如果你看得一头雾水，稍微提示一下：

我们是否能对图像上的一个点求斜率呢？

例如对于$A(1,1)$这个点，我们在它的左右各取一个点B、C，并逐渐靠近它:

PS: 从这里我开始尝试使用 GeoGebra 来作图，网页版的画图实在是太!蛋!疼!了!。。

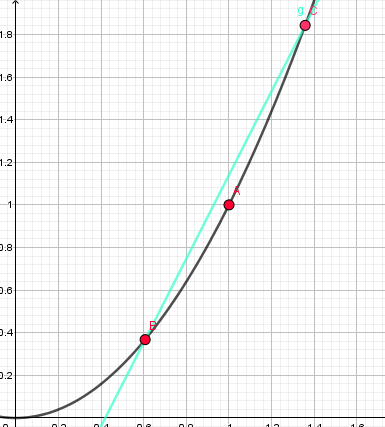
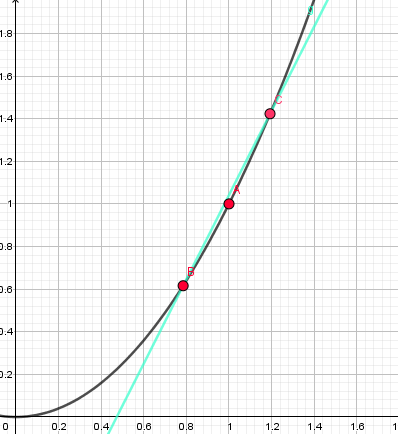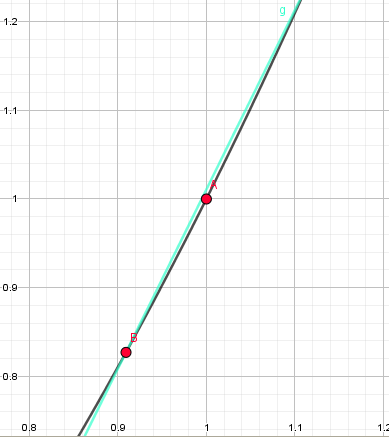
就这样不断靠近靠近。。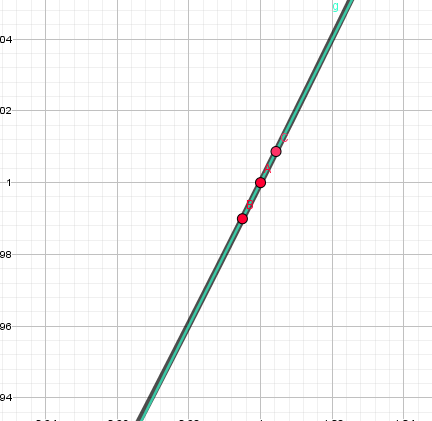终于，在N+N次逼近A点后，三个点几乎实现了重合: 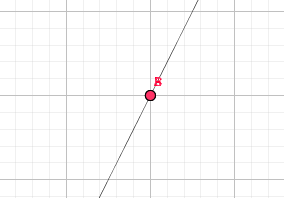注意，我这里之所以强调几乎，是因为它们确实没有碰上，只是它们之间的距离已经微小到了无穷的小。

此时，我们仍然能作直线$BC$，我们就称这条直线为点$A$在函数$y=x^2$上的切线。

好了，讲了这么多，我们可以回到原来的话题了。点A的斜率是多少？我相信，你已经心中有数了吧。

二次函数图像上的点A的斜率就是点A在这个函数图像上的切线的斜率。

这句话初看有点儿像句绕口令，多看几次才能搞明白。

(假设你已经看明白了，如果没有，你就假装看懂了 :) )

OK，那么接下来，让我们正式开始导数的学…哦不！可能还要加点料才行….

1.3 极限？

在介绍导数之前，我们还得弄懂另外一个概念:极限。极限，顾名思义，就是到达了极点的状态。比如说，考试还有1分钟就要结束时题目还没有答完时的感觉，或者暑假开学前的晚上猛补作业时的感受。人们在遇到极限时通常都会想:“不行了!不行了!”

但是，数学中的极限也是这个意思吗？如果指”不行了”“到头了”，又怎么能解决数学问题呢？事实上，数学中的极限的含义更加积极，它有”尽可能靠近”的意思，也就是无限地靠近。由于是数学，自然离不开数值了…所以，极限就是指一个数值尽可能地向另一个数靠近。

啥叫”尽可能地靠近”?举个例子，小明的家距离学校1000m，某天小明去上学，于是他与学校的距离变化如下:

1000m
∨
500m
∨
200m
∨
100m
∨
1m
∨
0.1m
∨
0.01m
∨
0.0000000000001m
...
∨
0.0000000000000000000000000001m

可以看到，小明与学校之间的距离越来越小，越来越靠近于 0m，但是就是到达不了 0m（~~因为他不想上学~~），于是我们就可以说

\[\lim_{距离 \to 0 m}\]

突然给出这么一个数学式子，你可能会一脸蒙蔽：这是个啥？
查查英汉词典可得知：Lim 原来是 Limit 的缩写，而 Limit 就是「极限」的意思。下面的小字里的「$\to$」表示「向 xxx 靠近」，所以这里的意思是”让距离这个值给我向 0m 尽可能地靠近!”

上面这个式子就表示距离无限地向$0\ m$靠近(但是就是到达不了$0\ m$!)

OKOK，理解了，那么让我们在式子上再加点花样吧!

\[\lim_{x \to a} f(x)=b\]

诶…更晕了…你可能会想：「这东西…现在我连符号都看不懂了！」
别急，让我再给你挨个儿解释解释！

首先看这个$f(x)$，这里的$f$是啥意思呢？其实很简单，f是单词“function”开头第一个字母，“function”就是函数的意思，所以$f$就是指某个函数。比如说一次函数，在初中学习中我们表示成

\[y=2x\]

想表示$x=1$时的值，我们得说

\[当x=1时,y=2\]

但是到了高中数学以及高等数学中，因为这样写起来太麻烦了，所以同一个函数，我们表示成

\[f(x)=2x\]

想表示$x=1$时的值，就可以简练地写成

\[f(1)=2\]

是不是很方便？

（顺便说一句，这里不一定必须用$f$作为函数的标识，如果你喜欢，也可以写

\[我真是酷毙了(x)=2x,我真是酷毙了(1)=2\]

）

回到上面的式子。$f(x)$就是以x为自变量的某个函数，在这里它到底是什么，我们不管它。
继续往下，下面的”$x \to a$“意思应该是”自变量x向a无限地靠近”。
这样，这个式子我们至少弄懂一半了，$\lim_{x \to a} f(x)$就是表示”对于$f(x)$这个函数，让$x$无限地逼近$a$“。
奇怪的是，式子的后面居然出现了等于号…小明上学时，与学校的距离也是一直在不停地变小啊…如果说是无限靠近$a$，又哪来的等于不等于呢？难道$f(x)$这么神奇，可以一边靠近，一边等于某个值吗？

这里就要提醒一下了:含有$lim$的式子里，所有”$=$“的意思都有一点小小的变动，不再表示”等于什么”，而是“靠近什么”。

所以啊，上面这个式子表示“当$x$无限地靠近$a$的时候，$f(x)$无限地靠近$b$”。
啪啪啪！第一个奇怪的数学符号，终于是被我们弄明白了！

1.3.1 小练习

稍微弄几道关于极限的题来做做吧…我们来找找感觉。

第一题

\[\lim_{x \to 1} x=？\]

唉…没什么难度嘛，直接把1代入进$x$算一下，结果就是$1$。

第二题

\[\lim_{x \to 3} x^2=？\]

稍微需要一点计算了，$3^2=3*3=9$，所以答案是$9$。

第三题

\[\lim_{x \to 0} (2x^2+5x+8)=？\]

似乎和第二题差不多么，只是计算有点麻烦了，列个式子算一下，$2x^2+5x+8=2*0^2+5*0+8=8$，结果是$8$。

第四题

你可能纳闷：这和一般的函数计算有什么区别？从哪里能体现出这个$lim$的特殊性？
来看这题：

\[\lim_{x \to 1} \frac{x^2-3x+2}{x-1}=？\]

妈呀，这题好像不能代入计算了？难道答案是$\frac2 0$吗？
不可能，分数的分母不能为0的…
那要怎么算呢？没有结果吗？
实际上，我们发现这个式子可以因式分解:

\[\frac{x^2-3x+2}{x-1}=\frac{(x-2)(x-1)}{x-1}=x-2\]

所以上面的题目就相当于

\[\lim_{x \to 1} (x-2)=？\]

答案就是$-1$。

这里你可能会说：$x-1$既然为0了，又怎么能约分上面的分数呢？
我们需要再看一遍极限的概念：一个数值尽可能地向另一个数靠近。这里的$x-1$准确地说，应该是一个非常非常接近于0，但不是0的值，所以是可以约分的。
这里用到了因式分解的技巧，算是比较麻烦的一题，我们暂时搁下，不深入讨论了。

1.3.2 额外的问答时间

你可能还有一些问题..让我尝试解答一下。

问：为什么代入数值，求得的就是它的极限呢？有什么理论依据吗？

答：这个问题比较难以解释，需要牵扯到函数的连续性之类的。我们还是按下不表，以免影响了本文的易懂性。

问：上面说极限的格式是 $\lim\limits_{x\to a} f(x)=b$，怎么后面又写成 $\lim\limits_{x\to 1} x=1$ 了呢？

答：格式里给出的写法是大概的、通用的写法，实际使用中我们不会写成

\[f(x)=x,\lim\limits_{x \to 1} f(x)=1\]

这么麻烦，直接用$x$代替极限格式中的$f(x)$，其潜台词也就是默认$f(x)=x$了。

1.4 斜率的计算

嗯，讲完了斜率的画法和极限的概念，我们可以综合一下这两个知识，开始真正的导数之旅了。

我们来看看斜率到底是怎么算出来的。我们仍然以这个函数图像$f(x)=x^2$为例。
如果我们设A点的坐标为$(x,f(x))$，那么C点坐标可以表示成$(x+h,f(x+h))$ (h是某个值)，这没问题吧？
那么

\[AC的斜率=\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}\]

如果你看到这个式子感到一脸懵，那么你得重新看看这张图了:
一次函数的斜率是某两点的竖直高度差除以水平高度差。类似地，AC的斜率我们也可以这么写。
继续我们的计算：

\[AC的斜率=\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}=\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}\]

这样，我们就得到了两点之间的斜率公式。

再进一步想想，我们要求出的是点A的斜率，光有两点的斜率公式要怎么办呢？

不管三七二十一，咱们先把数值代进式子里面再说。A点的坐标是（1,1），所以有

\[AC的斜率=\frac{f(1+h)-f(1)}{h}\]

这个式子看起来还是没法算啊…让我们稍微再化简一下，可以发现$f(1)=1^2=1，f(1+h)=(1+h)^2$。

所以这个式子还可以进一步化简：

\[AC的斜率=\frac{f(1+h)-f(1)}{h}=\frac{(1+h)^2-1}{h}\]

根据刚学到的完全平方公式，还可以再展开:

\[AC的斜率=\frac{(1+h)^2-1}{h}=\frac{h^2+2h+1-1}{h}=\frac{h^2+2h}{h}=h+2\]

这里的$h$是多少呢？

刚才讲到，$h$表示的是A点与C点横坐标的距离。而这两点，在前面就说到是非常非常接近的，所以$h$应该是一个很小很小的值。

很小很小…很接近很接近…有没有觉得这两句话有点熟悉？
。
。
。
。
。
。
。
。
。
。
。
。
。
没错！就是在极限？这一节里，我们简要地讲了如何正确处理数学里很接近的值。

关键的地方来了！$h$既然很小，我们就可以把上式加上$\lim$写成：

\[AC的斜率=\lim_{h \to 0}(h+2)\]

然后，后面这个式子的计算方式已经略熟悉啦，直接算出

\[AC的斜率=\lim_{h \to 0}(h+2)=2\]

这样，我们就终于得出了点A(1,1)在$f(x)=x^2$上的切线AC的斜率，也就是点A(1,1)在$f(x)=x^2$上的斜率。
看起来，计算一个点的斜率也没那么困难嘛！

1.4.1 小结

上面求斜率的过程可以概括成这几步：

在要求斜率的点$(x,f(x))$附近找出一个与它很靠近的点$(x+h,f(x+h))$！
把斜率用$\frac{C点纵坐标-A点纵坐标}{C点横坐标-A点横坐标}$表示出来！
在式子前面加上$\lim_{h \to 0}$，代入进去计算斜率！

1.4.2 通式

从上面的过程中我们可以看出，求某个点的斜率有固定的步骤和方法。依照这个方法，理论上来说我们可以求出任何函数上点的斜率。
接下来让我们试着找出这样一个公式，来表示任何函数$f(x)$上任意的点$(x,f(x))$的斜率，这样，以后进行计算时就很方便了。
这个过程并不困难。让我们用$f(x)$来代替上面的$1$就可以了。

\[斜率=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{(x+h)-x}}=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\]

这就是任意函数在某一点的一般斜率公式。呼，~~讲了这么多废话~~，我们总算开始步入正轨~~，而不是在各种概念上原地打转~~了。（哈哈）

记不住完整的公式也不要紧，需要用到的时候现场推导就可以了，理解这个有点复杂的式子才是关键。

1.4.3 求斜率有什么用？

我们已经基本掌握了求某一个点的斜率的方法。那么，这个东西有什么用处呢？
毕竟，如果没有实际用途的话，这样的数学工具看起来也没有什么意义啊…
在求导的用途中，最重要的也就是求某一点的切线的函数式。
因为用导数可以得出某一点的斜率，把斜率作为$k$代入$f(x)=kx+b$，很方便地能求出该点的切线方程。
实际上，在本文中我们就是用”某一点切线的斜率”来定义”某一点的斜率”的，是不？

依然以上面一节中的$f(x)=x^2$和点$A(1,1)$为例，我们来求一下A点的切线方程。

已经知道A点的斜率为2了，所以立即有

\[g(x)=2x+b\]

是A点的切线方程。

又知道这个方程经过A点，故使用待定系数法：

\[g(1)=2*1+b=1\]

解得

\[b=-1\]

所以A点的切线方程就是

\[g(x)=2x-1\]

这个结果对不对？画出来看看就知道有没有问题了。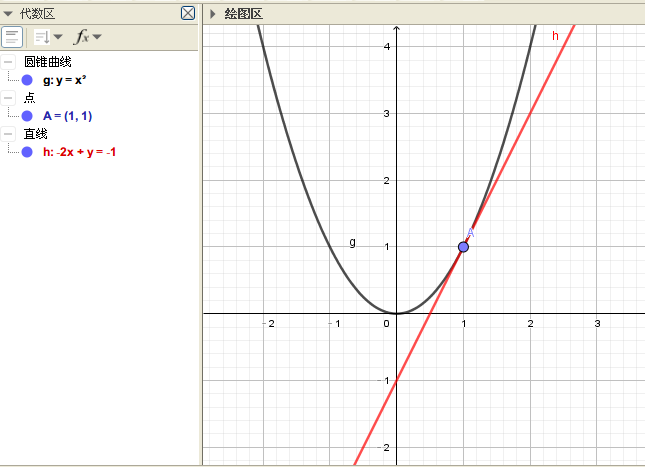图中红色的线就是我们刚刚求出的直线。看起来它的确是A点的切线。

另一个用途是求函数的最大/最小值。容易看出，上面这个函数的顶点$O(0,0)$的斜率为0。
因为顶点有”这一点的前后既不在上升，也不在下降”的性质，所以顶点的斜率都应该是0。
也就是说，只要找到一个函数中有一个斜率为0的点，就可以确定这一点是函数的一个顶点。

在接下来的导函数一节里，我们会讲得更多。

1.5 导函数

了解了导数和函数，这个”导函数”是个什么东西啊？别急，听我慢慢道来。

再看一眼这个式子：

\[\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\]

其实，这个式子就是$f(x)$的导函数。

函数是什么？我们复习一下函数的定义：

设A，B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数$y$和它对应，那么就称映射$f:x\to y$ 为从集合A到集合B的一个函数，记作$y=f(x)$。

不好意思拿错了，是这个：

在一个变化过程中，假设有两个变量x、y，如果对于任意一个x都有唯一确定的一个y和它对应，那么就称x是自变量，y是因变量，y是x的函数。

也就是说，只要有一个对应关系f，就可以说f是个函数。函是”匣子”的意思。把一个数$x$装进一个匣子，按照某个算式计算出另一个数字，就是函数。

因此，对f(x)求导的式子也是函数。这个函数，对于每一个x，计算出的结果都是$(x,f(x))$在$f(x)$上的斜率。需要求导的时候，我们就不用对每个数字都重新列式求一遍了，直接代入导函数就行，很方便。

导函数一般记作$f^{\prime}(x)$。

继续以$f(x)=x^2$为例，我们看看它的导函数长什么样子。
这次我们不代入任何值，直接运用上面的公式：

\[f^{\prime}(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}=\lim_{h \to 0}{\frac{(x+h)^2-x^2}{h}}\]

然后是

\[=\lim_{h \to 0}{\frac{x^2+2xh+h^2-x^2}{h}}=\lim_{h \to 0}{\frac{2xh+h^2}{h}}\]

最后

\[=\lim_{h \to 0}(2x+h)\]

又因为h靠近0，所以直接舍去，得到：

\[=\lim_{h \to 0}(2x+0)=2x\]

所以$f^{\prime}(x)=2x$。

仔细观察这个式子，我们发现它很有特点。
比如说想求$A(1,1)$斜率，我们也不用重新计算了，直接用导函数就行了。

\[A的斜率=f^{\prime}(1)=2\]

同理，想求$B(2,4)$斜率的话:

\[B的斜率=f^{\prime}(2)=4\]

是不是很方便？

导函数本身也是函数。所以对导函数$f^{\prime}(x)$求导还可以得到另一个函数，称为二阶导数，一般记作$f^{\prime\prime}(x)$。
当撇号过多时，比如说有个99999阶导数，直接记作$f^{(99999)}(x)$即可，不用打撇号了。

导函数有什么意义？只是为了装逼吗？
在了解这个问题之前，先想想导函数$f^{\prime}(x)$和函数$f(x)$之间的区别和联系。

项目	$f(x)$	$f^\prime(x)$
$x$对应的函数值$y$	是函数的值	是函数$f(x)$的图像上，横坐标为$x$的这一点的求导结果
是否是函数	是	是
求导结果	$f^\prime(x)$	$f^{\prime\prime}(x)$
函数零点的意义	无特殊意义	是$f(x)$的顶点的横坐标

(注：零点：函数的零点就是$函数=0$这个方程的解。比如$f(x)=x^2-1$的零点就是$x^2-1=0$的解，也就是$1$和$-1$ 。）

所以，导函数有一个重要的作用，就是计算函数的顶点坐标。
由于顶点的特殊性，该点的斜率是0，所以只要找出导函数$f^{\prime}(x)$的零点，相当于找到了顶点。

以$f(x)=ax^2+bx+c$为例。它求导的结果是$f^{\prime}(x)=2ax+b$。

$f^{\prime}(x)=0$的解就是$x=-\frac{b}{2a}$。这是不是与你在课堂上学到的二次函数的最值完全一致？

导函数的另一个作用是画函数草图。

前面已经说过，如果导函数$f^{\prime}(x)>0$，说明函数在这一点上的斜率是正的，也就是说，在这一点的前后，函数应该呈上升的趋势。
相反，如果$f^{\prime}(x)<0$，说明函数在这一点上的斜率是负的。在这一点的前后，函数应该呈下降的趋势。
于是乎，只要搞明白$f^{\prime}(x)$的图像，就可以把$f(x)$的图像画出来了。

举个例子，如果我们要画$f(x)=x^2+2$的草图，我们可以结合导函数这么画：

求导，得到$f^{\prime}(x)=2x$.
画出$f^{\prime}(x)=2x$的图像。
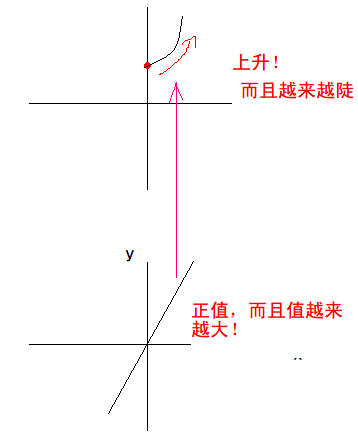
准备开始画图！先找出一个起点，这里我们取$f(0)$这一点，也就是$A(0,2)$。
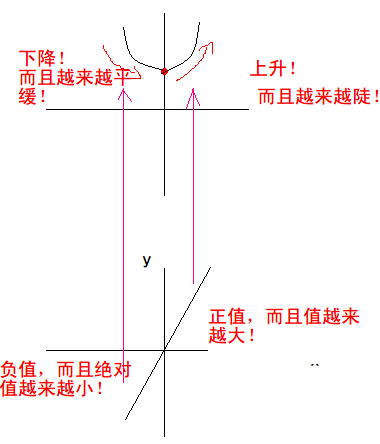
按照$f^{\prime}(x)$的图像所示，y轴的右边应该都是上升的，而且斜率越来越大，也就是：
同理，画出左半边：

这样就把$f(x)=x^2+2$的图像大概描出来了。
这题中导函数的优势还不能充分体现出来。遇到一些比较复杂的函数，一般结合导函数这样画图比较方便。

1.5.1 导数的表示方法

前面说到，导函数一般记作$f^{\prime}(x)$。
但是，实际上导函数还有一些常见的表示方法，这里介绍两种，以备后面的装逼使用。

第一种也就是刚刚讲的加撇号表示法。这种方法是在19世纪，一个叫约瑟夫·路易斯·拉格朗日的法国大叔发明的。

在他的表示法里，$y=f(x)$的导函数记作$f^{\prime}(x)$或者$y^{\prime}$。

这种表示方法非常常见，因为它写起来很容易，加个撇号只要花上你半秒钟的时间。

但是，它的弊端在于，如果有这么一个函数：

\[y=a+b\]

那么$y^{\prime}$表示什么？

$a$和$b$，到底谁才是自变量？谁是常量？

到底$y^{\prime}$表示是对$a$求导，还是对$b$求导？

不得而知。

要是有一种表示方法可以体现出对谁求导就好了。

这时，我们就需要第二种表示方法，也就是戈特弗里德·威廉·莱布尼茨，另一个德国大叔的写法。他也是微积分的主要创始人，他生活在17世纪，比上面那位要早几百年。
对$y=f(x)$关于$x$求导可以表示成：

\[\frac{dy}{dx},\frac{d}{dx}y,\frac{df(x)}{dx},\frac{d}{dx}f(x)\]

这些式子看起来很让人头晕…
(~~正因如此，他的符号至今仍在大学数学中频频现身。~~)
这里的$d$是Derivative(导数)的首字母。
式子的含义是对分母上的自变量，求分子上的函数的导数。

其中，$\frac{d}{dx}$可以看成是一个整体，它乘以谁，就是对谁求导。
例如：

\[\frac{d}{dx}x^2=2x\]

所以，如果我们想要表示导数的导数，也就是$f^{\prime\prime}(x)$，要怎么写呢？

就是：

\[f^{\prime\prime}(x)=\frac{d}{dx}\times\frac{d}{dx}\times y=\frac{d^2y}{dx^2}\]

分子上加平方的位置看起来怪怪的。而且d似乎也不遵循乘法定律。
你可能觉得莱布尼兹的方法很麻烦，但是在后面的章节里，你会逐渐明白这样表示的优点。

1.5.2 小结&补充

到现在为止，我们已经学会了：

斜率是什么&怎么算
导数是什么&怎么求
导函数是什么&怎么求

你可能还没有完全掌握以上内容，那也没关系！~
接下来我们会给出一些简单实用的公式，在你的学习过程中会频繁地使用它们来避免复杂的运算过程。一定要记牢！~

\[b^\prime=0\]

\[x^\prime=1\]

\[(kx)^\prime=k\]

\[(kx+b)^\prime=k\]

\[(ax^n)^\prime=anx^{n-1}\]

以上就是最基础的一组导数公式，其中$a和b$的含义是任意常数。

记住了它们，即使不会推算导数也可以轻松求出初高中大部分函数的导函数！

尤其是最后一个，堪称初等函数大杀器…

举个例子，要求出$y=2x^{999}$的导函数，直接用上面的公式：

\[y^{\prime}=2*999*x^{999-1}=1998x^{998}\]

是不是贼方便？

[选读]这里还有一些为学过三角函数的同学补充的：

\[(sinx)^\prime=cosx\]
\[(cosx)^\prime=-sinx\]
\[(tanx)^\prime=\frac{1}{(cosx)^2}\]

1.5.3 五年高考，三年模拟(雾)

总觉得应该来几道题目练练手…
虽然这样有点像老师上课的模式，有悖本文的初衷，但是练习一下真的能掌握不少…
废话少说，放题过来！
。
。
。
。
。
。
。
。

求出$f(x)=x^4-2x$的导函数。
求出$f(x)=(x+2)^{11}$的导函数。
求出$f(x)=x^{x}$的导函数。
求出$f(x)=\sqrt{x}$的导函数。
求出$f(x)=\sqrt[x]{x}$的导函数。
求出$f(x)=\sqrt[sin(x)]{x^{cos(x)}}$的导函数。
对于以上题目，你有什么感想？

作者的话：最近学业方面实在比较忙，先是期中考，又是统考月考周考什么的，今天刚参加全省联考…..(高二狗，体谅一下)说好的两个月完工也没下落了:(

2021年9月24日更新：作者回来啦！现在已经是一条大二狗了，国庆期间会重启更新~

1.5.4 导函数的四则运算

上面那几题已经让你晕头转向了？没关系！看完本节和下一节之后，你将可以很快地计算出它们~~从而去装B~~！

迄今为止，我们提到的例子都是一些比较简单的函数（额，当然上面的几题除外）。
基本上函数里都只有一个$x$。形式也就是$x+1$，$x^2$这样的，大家都学过了。

但是，平时遇到的函数可没这么简单，数学考试里当然不会直接出这样的玩意儿来考你。即便刚刚学过二次函数，你也应该已经遇到$f(x)=x^2+3x+2$或者$f(x)=(x-2)^2+3$这样的函数了。这种东西要怎么求导数呢？

其实很简单！不妨回忆一下下我们上面提到过的例子：

以$f(x)=ax^2+bx+c$为例。它求导的结果是$f^\prime(x)=2ax+b$。

（限时挑战任务！看看你能不能在 10 秒内找到这句话的出处:) ）

我们先不管结果是啥，只看每个部分。这个式子的每一部分我们都会求。$ax^2$的导数就是$2ax$，$bx$的导数就是$b$，$c$的导数……呃呃，一个常数的导数，永远是$0$嘛。

所以……它的导数就是$2ax+b$？看起来确实是这样。

我们不妨大胆猜测一下：求一个里面有加号的函数的导数，只要求出各个部分的导数，然后加起来就好啦！

然而事实是怎样呢？事实是……我们的猜测是对的。导数的加法就是可以这么拆开计算的。

写成公式的方式就是：

\[(A+B)^\prime=A^\prime+B^\prime\]

（别忘了一撇「$\prime$」的含义哦，它是指对这个式子求导。）

那么，这是为啥呢？这个问题我们稍微往后放放，你在后面的选读部分会看到它的证明。

我们先看看利用这个，能不能做出上面的题了。

第一题是$f(x)=x^4-2x$。
它的第一部分求导是$4x^3$（别忘了这个公式哟：$(ax^n)^\prime=anx^{n-1}$）,第二部分的导数是$2$。所以结果就是$4x^3+2$。

第二题是$f(x)=(x+2)^{11}$……额，这个怎么办呢？

其实只要一点一点乘开就好了！打开我们的 Maple，输入函数，点击展开：然后按上面的方法，对每个部分求导就好了！

你可能会说：$(x+2)^{11}=(x+2)(x+2)(x+2)(x+2)(x+2)...$，这么长的式子，考试的时候要展开不得累死我？

当然，这种暴力算法虽然不能实用，但是至少是可以算出来的。如果遇到这样的函数，展开是最差劲的选择，但起码是一种选择……起码是可以算出来的，是吧？

这种方法显然太蠢了。有没有更妙的方法来计算第二题呢？这就进入到咱们今天的重头戏：复合运算！

。
。
。

诶还没进呢，没看到标题是「四则运算」吗？等下一节吧（顶级拉扯）

加法已经说完了，我们来看看乘法吧。

（大家读到这里可能比较突兀，因为上面的练习里面忘了出相关的题了。偏偏这个乘法运算又很重要，还是希望大家快速过一遍！不要跳过哈，不然你待会儿会后悔的，哼哼）

什么叫乘法运算呢？举个例子：

\[f(x)=(x^3+3x+3)(x^2+2x+2)\]

这个函数怎么求导呢？有同学可能会说：加法是分开加，那我乘法也分开乘嘛！先对$x^3+3x+3$求导，再对$x^2+2x+2$求导，然后乘起来就好了吧？

但是，But，这样是完全错误的哦！不如再想想？先乘开自己求导一下，再找找规律？

算啦算啦，我知道你很想知道，先把正解放在这里：

\[f^\prime(x)=(x^3+3x+3)^\prime(x^2+2x+2)+(x^3+3x+3)(x^2+2x+2)^\prime\]

\[=(3x^2+3)(x^2+2x+2)+(x^3+3x+3)(2x+2)\]

这就是说，乘法的规则和加法完全不同，它的导数是对第一个式子求导，乘第二个；再对第二个式子求导，乘第一个。然后加起来。
写成公式的方式就是：

\[(AB)^\prime=AB^\prime+A^\prime B\]

或者写得再「专业」一点：

\[(f(x)g(x))^\prime=f^\prime(x)g(x)+f(x)g^\prime(x)\]

先尝试理解一下这个式子哈。
我知道你的心里肯定装满了大大的问号：凭啥这么算？你这是个啥计算方法？你这样算出来，真的是对的嘛？

很不幸的是，它确实是对的。凭什么呢？
这就有点超过知识范围了。
我一起放在下面的选读部分吧，如果你自认为可以，不妨挑战一下阅读！应该……不会需要太高的数学水平？（这个挑战就没有上面的「习题」那么坑了，哈哈！）

[选读] 加法求导公式的证明
要证明对两个函数$f(x)$和$g(x)$，可以推出$(f(x)+g(x))^\prime=f^{\prime}(x)+g^{\prime}(x)$。
先回顾公式：

\[f^{\prime}(x)=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}\]
，

所以写出$(f(x)+g(x))^\prime$的求导式子，然后摆弄一下式子的加法顺序：

\[\begin{aligned}(f(x)+g(x))^\prime\\&=\lim_{h \to 0}{\frac{(f(x+h)+g(x+h))-(f(x)+g(x))}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)+g(x+h)-f(x)-g(x)}{h}}\\&=\lim_{h \to 0}{\frac{(f(x+h)-f(x))+(g(x+h)-g(x))}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)-f(x)}{h}}+{\frac{g(x+h)-g(x)}{h}}\\&=f^{\prime}(x)+g^{\prime}(x)\end{aligned}\]
这就证完了！

[选读] 乘法求导公式的证明
要证明对两个函数$f(x)$和$g(x)$，可以推出$(f(x)g(x))^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)$。
还是写出$(f(x)g(x))^{\prime}$的求导式子：

\[(f(x)g(x))^{\prime}=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}\]
呃，这里不太好办了……只有两项，怎么玩它呢？
其实可以试试「凑项」！具体来说，就是加一个什么东西，再减去它，这样式子依然不会变，就像$123+1-1$还是$123$一样！

我们这里要凑进去的是$f(x+h)g(x)$，详细地说就是凑成下面这样：

\[\begin{aligned}(f(x)g(x))^{\prime}\\&=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h}}\\&=\lim_{h \to 0}{\frac{f(x+h)(g(x+h)-g(x))+(f(x+h)-f(x))g(x)}{h}}\\&=\lim_{h \to 0}{f(x+h)\frac{g(x+h)-g(x)}{h}}+\frac{f(x+h)-f(x)}{h}g(x)\\&=f(x+h)g^{\prime}(x)+f^{\prime}(x)g(x)\end{aligned}\]
注意，h是无限趋近于0的，所以上式也就是$f(x)g^{\prime}(x)+f^{\prime}(x)g(x)$了。

PS：这两个证明乍一看很麻烦，但是自己动手写一遍，你会发现还挺简洁的……

2023年2月13日更新：啊，迟来的更新！

到这里为止，我们已经介绍了含有加法和乘法的导数计算，总结一下：

对于加法，我们可以用加法求导公式： $\begin{aligned}(f(x)+g(x))^\prime&=f^{\prime}(x)+g^{\prime}(x)\end{aligned}$；
对于乘法，我们可以用乘法求导公式：
$\begin{aligned}(f(x)g(x))^{\prime}&=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)\end{aligned}$。

接下来是减法和除法。加法和减法是一对同胞兄弟，掌握了带加法的求导，带减法的求导就非常顺理成章了：

\[(f(x)-g(x))^\prime=f^{\prime}(x)-g^{\prime}(x)\]

为什么是这样呢？因为减法可以转化为加法，比如$3-2=3+(-2)$，所以和加法的求导公式非常类似，只不过是把加号换成了减号而已。

更严格的证明可以这么想：利用负数，我们就可以把减法全部变成加法：

\[f(x)-g(x)=f(x)+(-1)\times g(x),\]

而这时就可以利用加法求导公式了。

如果你问 $\left[(-1)\times g(x)\right]'$ 是什么，不妨再看看 1.5.2 节给你的简单实用的公式？
（然后你就会知道 $\left[(-1)\times g(x)\right]'=-1\times g'(x)=-g'(x)$ 了。要时常回顾之前学过的东西哦！）

只要利用一下加法求导公式，其实就已经得到上面的减法求导公式了。这样，四则运算里的三个求导公式就都证明完了！

然而，除法这个看起来平平无奇的运算，求导却是最难的。为了证明它，上面所有的知识甚至都还不够，我们还需要用到一个（刚刚提了一嘴的）新概念：复合函数。下一节我们就来讲讲复合函数和它的求导。

1.5.5 复合函数的导函数

你也许火急火燎地翻过了上面的证明，想要知道复合函数的求导公式是什么。在了解求导公式之前，我们先来看看复合函数是什么。

最直观地说，复合函数就是把一个函数「塞」到另一个函数里面去，然后把它们合并成一个新的函数。

比如，我们把函数$f(x)=x^2$「塞」到函数$g(x)=x+1$里面去，就得到了一个新的函数$h(x)=g(f(x))=x^2+1$。这个新函数$h(x)$就被称为$f(x)$和$g(x)$的复合函数。

这里，$f(x)$替代了$g(x)$的式子里的$x$的位置，所以才写成了$g(f(x))$。意思就是：$g$这个因变量，它的自变量现在不叫$x$了，而是全部替换成$f(x)$。既然 $g(x)$ 是

\[g(x)=x+1,\]

那$g(f(x))$的式子理应是：

\[g(f(x))=f(x)+1.\]

既然 $f(x)=x^2$，那么$g(f(x))$的式子就进一步可以代换成：

\[g(f(x))=x^2+1.\]

有人可能会问：你把自变量从$x$换成了$f(x)$，那原来的因变量 $g$ 不就变了吗？这么说对也不对。

[提示]

下面这一部分是对函数的深入讲解，如果你觉得有些难以理解，可以先跳过，等到后面再回来看。

在高等数学里，我们不再提「因变量」和「自变量」这两个概念了，而是用「函数」和「变量」来代替。函数的括号里一定是一个字母吗？未必。函数括号里的就得是一个变量吗？也未必。我们已经见过很多种写法：

$f(x)$：代表一个函数，它的自变量是$x$；
$f(1)$：代表令函数$f(x)$的自变量$x$等于1时的函数值；
$f(g(x))$：代表令函数$f(x)$的自变量$x$等于另一个函数$g(x)$时的函数。

说白了，函数只是一个黑盒子，你不清楚里面的计算过程，只能往里面塞一个东西，然后得知它计算出的东西。

它的括号里是你可以塞进去的东西，你想塞什么都可以。你塞进去一个变量 $x$，根据计算结果就知道这个函数和 $x$ 有什么关系了；你塞进去一个函数 $g(x)$，根据计算结果就知道这个函数和 $g(x)$ 有什么关系了；你塞进去一个值 $1$，根据计算结果就知道这个函数和 $1$ 有什么关系了。

注意，这里的「计算结果」并不一定和你塞进去的东西直接有关系。不是说你塞进去值就一定得到值，也不是说塞进去变量就一定还是函数。比如这个函数：$f(x)=x^2+y$。把 1 塞进去，你会得到：

\[f(1)=1^2+y=1+y.\]

你可能会奇怪：$f(1)$ 怎么不是一个数字，而是含有一个未知字母 $y$ 的式子呢？这也能被称为一个函数吗？答案是：当然可以。函数这个黑盒子只能保证两条规则：

你塞进去一个未知量，就一定能得知黑盒子的全貌。比如你塞进去一个变量 $x$，就能得知这个函数和其他任何量有什么关系，也清楚明白地知道黑盒子的运作原理了：$f$ 其实就是把塞进去的东西平方，然后再加上一个未知量 $y$ 嘛！
它计算出的东西一定是一个式子。当然，这个式子里可能有整数，有小数，有加减乘除，甚至有未知量，但它一定是一个式子。除此之外，函数不会给你任何保证。你塞进去一个值，它或许会给你一个值，也或许会给你一个式子。

这就是为什么我们可以写出$g(f(x))$这种东西的原因。$g$是一个黑盒子，我们把$f(x)$塞给它（或者说，把$x^2$塞给它），它根据和塞给它$x$时一样的工作原理，计算出了一个式子。这个式子里有一个未知量 $x$，所以我们说$g(f(x))=x^2+1$。

回归正题，讲讲复合函数的求导。这个求导公式是：

\[\left[g(f(x))\right]'=g'(f(x))f'(x).\]

这个公式的意思是：复合函数的导数等于里面的函数的导数乘以外面的函数的导数。

啊，又是一个和乘法求导公式一样拗口的公式！

[选读] 复合函数求导公式的证明

它的证明过程也是很复杂的，考虑到网上两三步证完的基本都是错误证明（包括高中课本上的），而在严格的分析法里需要考虑诸多细节，可能你也不想看（即便是高中数学水平，硬着头皮也未必能看懂），所以这里只能扔个链接给你：复合函数求导公式的证明，如果闲着没事，可以看看。

PS：说复杂，其实也不复杂，主要是有很多边边角角的情况需要分类讨论，每一种单独证明，因此汇成了一篇长篇大论……

不过，这个公式的意思其实很简单。我们继续说上面$f(x)=x^2, g(x)=x+1$的例子。要分几步走来计算：

先计算$f(x)$的导数，得到$f'(x)=2x$；
再计算$g(x)$的导数，得到$g'(x)=1$；
然后计算$g'(f(x))$，得到$g'(f(x))=1$（因为 $g'(x)$ 是一个常函数，你把 $x$ 换成任何值，它都给你 $1$！）；
最后，计算$g'(f(x))f'(x)$，得到$g'(f(x))\times f'(x)=1\times 2x=2x$；
所以，最终的答案是$\left[g(f(x))\right]'=2x$。

这个结果和我们直接对$g(f(x))=x^2+1$等式右边的$x^2+1$求导数的结果是一样的。

现在，让我们再试试前一节的问题：$(x+2)^{11}$的导数是多少？我们可以把它拆成复合函数的形式：

\[f(x)=x+2, g(x)=x^{11},\]

那么$g(f(x))$就是$(x+2)^{11}$。这下我们只要计算$g(f(x))$这个复合函数的导数就可以了：

先计算$f(x)$的导数，得到$f'(x)=1$；
再计算$g(x)$的导数，得到$g'(x)=11x^{10}$；
然后计算$g'(f(x))$，得到$g'(f(x))=11(x+2)^{10}$；
最后，计算$g'(f(x))f'(x)$，得到$g'(f(x))\times f'(x)=11(x+2)^{10}\times 1=11(x+2)^{10}$；
所以，最终的答案是$\left[g(f(x))\right]'=11(x+2)^{10}$。

这样，我们就把复合函数的求导问题转化成了两个简单的函数求导问题，然后几步就完成了这个函数的求导。化繁为简，这就是复合函数的求导的核心意义。

1.5.6 导函数的除法运算

虽然除法和乘法也是一对反义词，但它们的求导公式是完全不同的。除法的求导可以说是最难的，所以我们单独拿出来讲。

它为什么困难呢？上面我们证明减法求导的时候，是把减法转化成加法和乘负一（更「专业」的说法是乘 相反数 ，如果你学过这个词的话），然后利用加法求导公式得到的。你肯定很容易想到：那么，除法求导的时候，我们是不是可以把除法转化成乘法和乘一个什么东西呢？

答案是：不可以。首先我们要知道，运算是有好几个不同层次的，最低级的是加减，而乘除是比它们俩高一层的。 注意注意！看「减法可以转化成加法和乘负一」这句话里的几个词：

减法可以转化成加法和乘负一

这里的「减」和「加」是相对应的，而「乘」是比加减更高一层的计算！

而我们想象的：

除法可以转化成乘法和乘一个什么东西

这里的「除」和「乘」是相对应的，但是「乘」不是比乘除更高一层的计算！

所以，想要对应上前一节的思考方式，也应该是：

除法可以转化成乘法和 XXX 一个什么东西

其中的「XXX」必须得是一种比乘除法还要高一层的计算才合理。

这个超高级的计算是什么呢？就是幂运算！所以，除法求导的时候，我们应当把除法转化成乘法和乘一个幂运算的结果：

除法可以转化成乘法和对负一的幂运算

或者用更简单的数学语言来说，就是：

\[\frac{f(x)}{g(x)}=f(x)\times \left[g(x)\right]^{-1}.\]

注意

$\left[g(x)\right]^{\text{xxx}}$ 我们习惯上简写成 $g^{\text{xxx}}(x)$，这里用方括号括起来是方便你理解的。后面我们就不再用方括号，直接写成 $g^{\text{xxx}}(x)$ 了。

接下来让我们仿照算减法求导公式时的做法，利用一下乘法求导公式！我们知道，乘法的规则是对第一个式子求导，乘第二个；再对第二个式子求导，乘第一个。然后加起来。

「对第一个式子求导，乘第二个」是：

\[f^{\prime}(x)\times g^{-1}(x),\]

唔，这部分看起来很简单嘛！

「对第二个式子求导，乘第一个」是：

\[f(x)\times \left[g^{-1}(x)\right]',\]

新问题又来了，这里的 $g^{-1}(x)$ 怎么求导呢？我们好像没有学过这个东西啊！

别急，再想想，既然气氛都烘托到这了，肯定是有办法的。

我们到底在哪里提过关于幂的求导呢？
我们到底在哪里提过关于幂的求导呢？
我们到底在哪里提过关于幂的求导呢？

在继续之前，请你再三思考一下，翻一翻之前的内容，看看有没有提到过，然后再往下看。

。
。
。
。
。
。
。
。
。
。
。
。
。
。
。

没错，还是在 1.5.2 节给你的简单实用的公式表里面，有关于幂的求导公式，而且当时我们还叫它「初等函数大杀器」呢：

\[(ax^n)'=nax^{n-1}.\]

这个式子是说，对于 $ax^n$ 这个式子，它的导数是 $nax^{n-1}$。比如，对于 $x^2$，它的导数是 $2x^{2-1}$；对于 $2x^3$，它的导数是 $2\times 3x^{3-1}$。

所以，看起来我们可以对于 $[g(x)]^{-1}$ 用上面的公式求导。有个小问题是：$g(x)$ 并不是 $x$ 啊？那我们怎么用呢？

这里要用到我们的另一个大杀器了：复合函数。我们可以令 $f(x)=x^{-1}$，那 $[g(x)]^{-1}$ 不就是 $f(g(x))$ 了吗？

来试试看！我们把复合函数的求导公式代入进去。首先计算 $f(x)$ 的导数：

\[f'(x)=\left(x^{-1}\right)'=-1\times x^{-2} = -x^{-2}.\]

注意，这里的 $x^{-2}$ 其实就是 $\frac{1}{x^2}$，所以 $f'(x)=-\frac{1}{x^2}$。那么，$f'(g(x))=-\frac{1}{g^2(x)}$。

所以呢，我们可以继续按照复合函数的求导公式来计算：

\[ \begin{aligned} \left(\left[g(x)\right]^{-1}\right)'&=[f(g(x))]'\\ &=f'(g(x))g'(x)\\ &=-\frac{1}{g^2(x)}\times g'(x)\\ \end{aligned} \]

看起来我们终于解决了 $[g(x)]^{-1}$ 的导数，它就是 $-\frac{1}{g^2(x)}g'(x)$。耶✌！

乘胜追击，让我们完成这个绕了山路十八弯的除法求导公式。「对第二个式子求导，乘第一个」现在就是：

\[f(x)\times \left[g^{-1}(x)\right]'=-f(x)\frac{1}{g^2(x)}g'(x).\]

所以，最终的除法求导公式是把它和「对第一个式子求导，乘第二个」加起来，也就是下面两个加起来：

\[-f(x)\frac{1}{g^2(x)}g'(x)+f^{\prime}(x)\times g^{-1}(x)\]

经过一串草稿纸上的暴力分母通分，我们得到了最终的除法求导公式：

\[\left[\frac{f(x)}{g(x)}\right]'=\frac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{g^2(x)}.\]

真是「道路阻且长」啊。折腾了这么多得到的除法公式，结果还这么复杂，大概可以排进我们心目中「我最讨厌的导数公式」前三名了吧？

再小结一下，到目前为止，我们已经学会了求导的以下几种方法：

一些通用的求导公式
加减乘除的求导公式
复合函数的求导公式

对于水平稍高的同学，现在已经可以回头完成我们的「五年高考，三年模拟」了。快去试试吧（笑）下次更新会公布正确答案。

PS：下一次更新将在本周内，敬请期待~

w568w

梦想改变自己的疯子。

项目	\(f(x)\)	\(f^\prime(x)\)
\(x\)对应的函数值\(y\)	是函数的值	是函数\(f(x)\)的图像上，横坐标为\(x\)的这一点的求导结果
是否是函数	是	是
求导结果	\(f^\prime(x)\)	\(f^{\prime\prime}(x)\)
函数零点的意义	无特殊意义	是\(f(x)\)的顶点的横坐标